The Principle of Nominality

Here we examine how JM Hurst arrived at the framework we often use to perform phasing analysis on financial markets

What is Nominality?

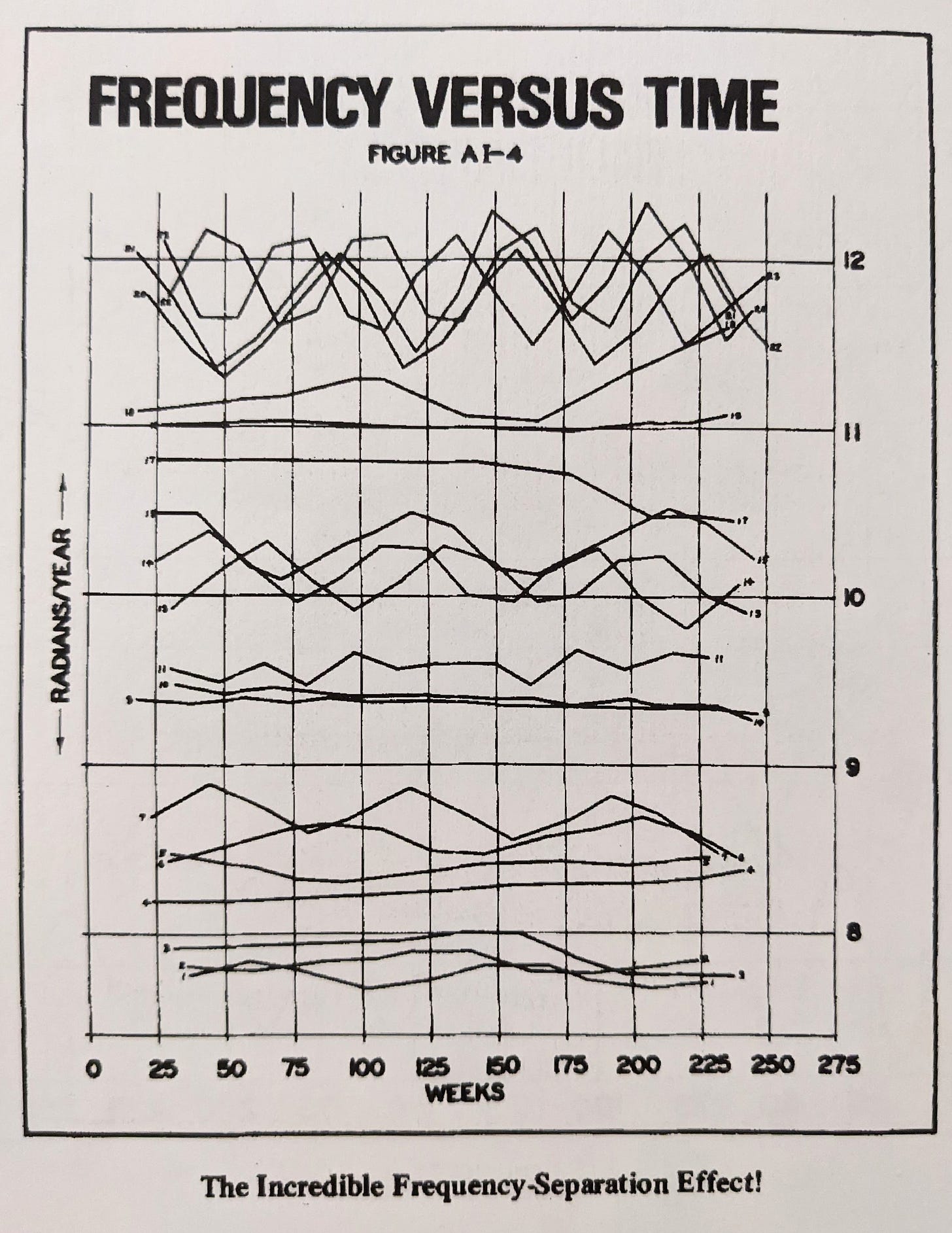
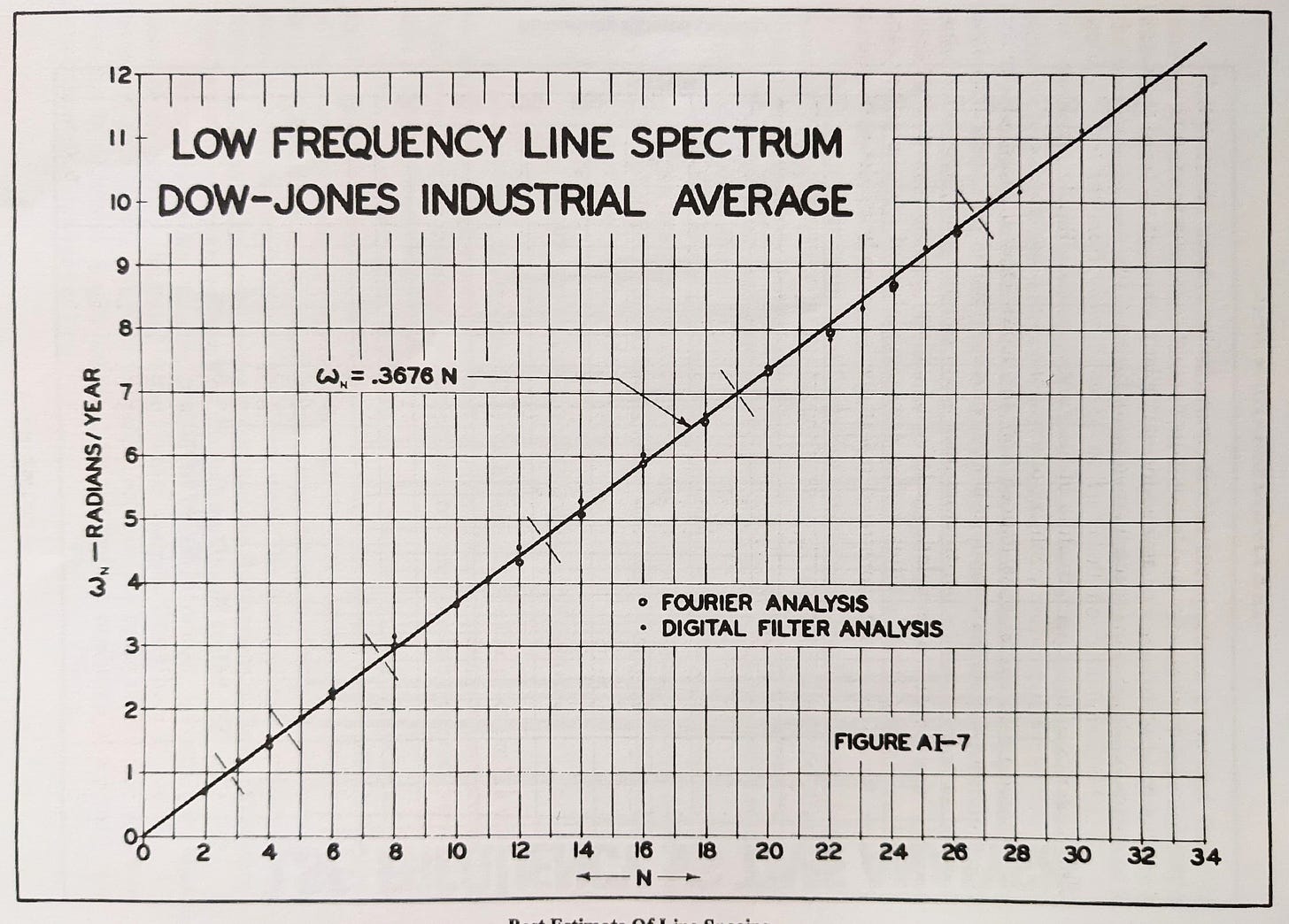
The term ‘nominal’, in relation to Hurst Cycles, refers to the distinct naming convention of groups in Hurst’s nominal model. These are a collection of groups that coalesce around similar frequencies, named for ease of use and convention. In reality, periodic functions in financial markets are plagued by all kinds of variation, excursions from the nominal model groups are described by the principle of variation. These variations are comprised of both frequency and amplitude modulation. Hurst referred to this variation as ‘magnitude-duration-fluctuation’. Catchy!

Importantly, Hurst found in his research that the grouping of component frequencies exhibited in stockmarkets (and commodities later in the Cycles Course) show distinct spectral spacing. Another way to describe the spacing of frequencies is that of a non normal distribution. The latter might indicate that markets are infact entirely explained by ‘pink noise’ - the type of noise that displays a distinct ‘1/f’ magnitude spectrum in the frequency domain. The spectral spacing gave rise to the grouping described above and the resulting nominal model. The groups within the nominal model can also be thought of as ‘carrier’ frequencies, each one consisting of finer frequencies closely related to the carrier and suitably amplitude modulated.

In the ‘Profit Magic for Stock Transation Timing’, Hurst applied a number of spectral analysis methods to stockmarket indices and issues. Above, the output of comb filter analysis reveals distinct spectral groupings. Courtesy: Traders Press.

Here the average spectral spacing between nominal model groups is explored via a comparison of static fourier transforms and comb filtering output. It was found to be 0.3676 radians per year in the DJIA. Courtesy: Traders Press

---